光と色の話 第一部
第8回 照度の性質
「照度」の距離依存性と入射角依存性について
はじめに
「照度」は、着目した面の“照らされ度合い”のことでしたね。正確に言えば、光が入射する面の単位面積当りの光束、ということになります。各種測光量の中で、照度は我々の身の回りの照明にとって特に重要で、馴染みの深いものです。また、マシンビジョンにおいても、ワークを照明する条件として重要です。今回は、照度の重要な特性である、距離依存性と入射角依存性についてお話します。
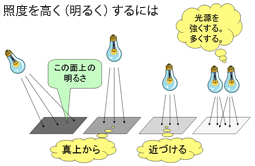
照度と距離の関係 ・・・・・ 照度に関する距離の逆2乗則
我々の生活体験から、その面を照らす光源が遠くなれば、その面の明るさは暗くなる、ということは誰でも知っています。例えば読み書きをする机上の「明るさ」は電気スタンドが近い方が明るくなりますね。
「照度」に関する重要な特性として、光源の大きさが十分小さい（点光源と見做せる）場合、その面の照度は光源からの距離の 2 乗に反比例する、という法則があります。具体的にもう少し詳しく考えて行きましょう。
今、四方八方に均等に光を放出する充分小さい光源（点光源）を想定します。この点光源からは放射状に光が発散放出されています。この点光源から或る立体角範囲に放出される光束は放射状に広がりながら進行していきますので、その光束が照らす「面積」は距離比の 2 乗に比例することになります。つまり距離が遠くなる程、同じ光束でより広い（距離の 2 乗倍の）面積を照明することになりますので、結局、照度すなわち単位面積当りの光束は距離比の 2 乗分の 1 になってしまう訳です。
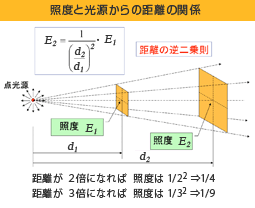
数式で書くと分かりにくくなってしまいますが、距離が 2 倍になれば照度は 1 / 22 = 1 / 4 に、距離が 3 倍になれば照度は
1 / 32 = 1 / 9 になり、逆に距離が 1 / 2 になれば照度は 22 = 4 倍に、距離が 1 / 3 になれば照度は 32 = 9 倍 になる、と考えれば分かり易いと思います。これが照度に関する距離の逆 2 乗則です。
この法則を適用して、太陽系の各惑星上での真昼の明るさを概略計算してみた結果を≪※1≫に示します。 この法則が成り立つのは、勿論理想的な場合、すなわち「拡散性（四方八方に均等に光を発散している）」の「点光源」の場合≪※2≫であって、実際の光源の場合には光源の大きさがあり、光の放射方向によって強さが異なる場合も多いため、厳密には理想通りにはならず、この理論式からの誤差が出てきます≪※3≫。通常の発散性の光源の場合、大雑把に言って、光源の大きさ（径）に対してその 10 倍以上の距離であれば概ねこの法則（照度に関する距離の逆 2 乗則）が成り立つと考えても良いでしょう。
照度と入射角との関係 ・・・・・ 照度のコサイン特性
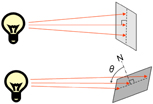
光源から或る距離にある面を照明したときの照度は、その面を光の進行方向に垂直にした時が最も明るくなり、その面を傾けると暗くなりますね。照度はその面に入射する光の入射角 θ の余弦（ cos θ ）に比例して変化する、という重要な性質があります。
これを照度の斜入射光特性（コサイン特性）と呼んでいます。
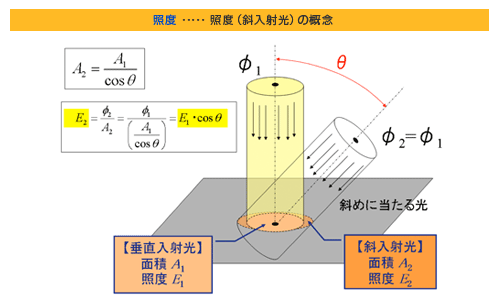
今、円柱状の平行光（光束 φ1 ）が照射面に垂直に入射している場合を考えます。この時の面上の照射面積を A1 、照度を E1 としますと、照度の定義より
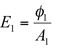
と書けます。一方、この平行光を照射面に斜め方向（入射角 θ ）から入射させた場合を考えます。この時の面上の照射面積を A2 、照度を E2 とします。（光束は変化しませんから φ2 ＝ φ1 です。）斜め方向から照射した場合は、照射面が円柱を斜めに切断する形になりますから
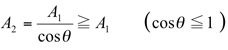
すなわち、垂直入射のときより広い面積を同じ光束（ φ2 ＝ φ1 ）で照明していることになりますから、照度は垂直方向から照明した時より低くなります。 具体的には、斜め方向から照明した時の照度 E2 は、上記の幾何学的な関係から理論的に、
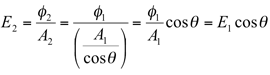
ということになります。
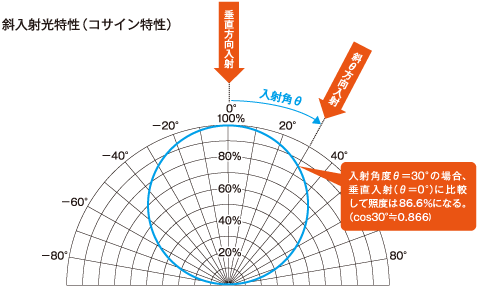
つまり、斜め θ 方向から照明した時の照度（ E2 ）は、垂直方向から照明した時の照度（ E1 ）の cosθ 倍になる、という重要な性質が導かれました。これを図示すると下のグラフのようになります。夏が暑く冬が寒い理由も、この「斜入射光特性（コサイン特性）」の結果として説明されます。≪※4≫
微小面光源による被照明平面の照度分布 ・・・・・ コサイン 4 乗則
上記の、照度に関する「距離の逆 2 乗則」と「斜入射光特性（コサイン特性）」から、照明光学系としての重要な特性である、「コサイン 4 乗則」が導かれます。 「コサイン 4 乗則」とは、拡散性の微小面光源で対向する平面を照明した場合、光源から垂直な対向面の照度(直下照度 E0 ) に対して、角度 θ 方向の面上の照度
( Eθ ) は、cos4θ 倍になる、というものです。数式で書けば
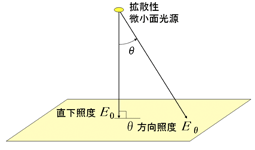
Eθ = E0・cos4 θ
となります。≪※5≫
これは、平面を照明する場合の照度分布を見積る場合の指針となる重要な関係式です。 直下（ 0° 方向）の照度に比べて、周辺へ行くほど照度が急激に低下することを示しています。 例えば、 30° 方向の平面上の照度はおよそ半分強に、 45° 方向の照度は 4 分の 1 になってしまいます。 実際の光源の場合は、一言で拡散性と言っても、その配光特性は様々であり、この理論通りになるとは限りませんが、大雑把な傾向を示す目安として知っておくと便利です。
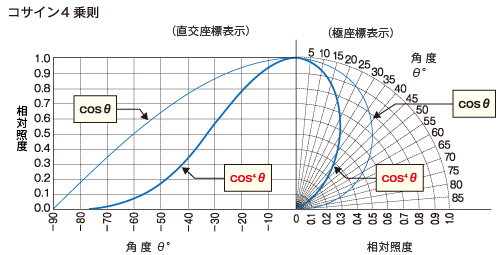
LED 照明などの場合には、配光特性が拡散性とは言い切れない（指向性が強い）場合も多くあり、そのような場合には cos4θ よりももっと急激に照度が低下し、半ばスポット照明のような照度分布になってしまう場合もあります。
今回の照度の性質は、分光的条件には無関係で、幾何学的条件によって決まりますので、放射照度（センサー照度）に対しても全く共通しています。
注釈
≪※1≫ 冥王星での真昼の明るさはどのくらい?
具体的な例を挙げて大雑把な計算をしてみましょう。我々の地球は太陽からの光を受けて昼夜の明るさを得ていますね。地表の照度は、地球上の位置（緯度）や時刻、天候などの状況によって色々ですが、日本の真夏の晴天真昼間の最大照度は十数万 lx 程度と言われています。仮に 10 万 lx とした場合、この条件下で、他の惑星ではどのくらいの照度になっているのでしょうか?
当然惑星表面の照度はその惑星を取り巻く大気や天候や諸々の条件によって変わると思われますが、それらは一切無視して、大気層も無いものと仮定して計算してみましょう。
太陽から地球までの距離はおよそ 1 億 5000 万 km で、 10 万 lx の照度になっています。太陽から火星までの距離はおよそ 2 億 2300 万 km ということですので地球の場合との距離比は約 1.5 倍、従って火星では照度が
10 万 lx × 1 / 1.52 ≒ 4 万 5000 lx 位となります。 同様にして、太陽・土星間の距離はおよそ 15 億 km、太陽・冥王星間の距離はおよそ 60 億 km とのことですので、地球の場合との距離比はそれぞれ 10 倍、および 40 倍になります。従って、照度はそれぞれ地球の照度（ 10 万 lx ）の 1 / 102 ＝ 1 / 100 および
1 / 402 = 1 / 1600 、すなわち、 1000 lx および 60 lx という計算になります。
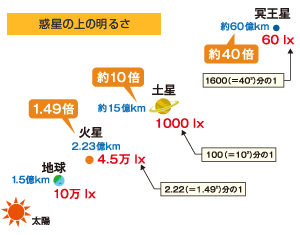
つまり、地球上で真夏のカンカン照りで 10 万 lx の照度のときでも、冥王星では 60 lx 程度、すなわち、通常の作業机の下の空間くらいの薄暗さになっているという感じですね。 （なお、冥王星は 1930 年に発見されて以来、太陽系の第 9 惑星とされていましたが、 2006 年に国際天文学連合総会で準惑星という位置付けに変更されました。）
≪※2≫ 照度に関する距離の2乗則の理論的導出
照度に関する距離の逆 2 乗則は、光度、照度、および立体角の定義から理論的に導き出されます。
光度Iの定義は、単位立体角当りの光束で
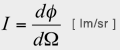
照度の定義は、単位面積当りの光束で、
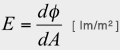
立体角の定義は、球面上の単位面積を球の半径の 2 乗で割ったもので、
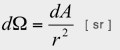
でした。従って、これらの 3 つの定義式から
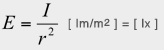
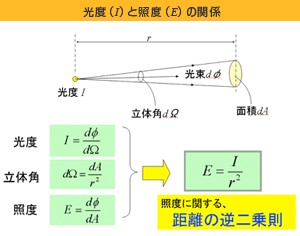
すなわち、照度は光度に比例し、距離の 2 乗に逆比例する、という理論式が導かれます。 ただし、拡散性点光源（光源の面積が無限小）であることがこの法則の前提条件です。
≪※3≫ 照度に関する距離の逆 2 乗則の誤差
照度に関する距離の逆 2 乗則は、厳密には四方八方に均等に光を発散している「点光源」に対して理論的に成立する法則です。実際の光源は当然「点光源」ではなく、ある大きさを持っていますし、配光特性も全方向に対して均等という訳ではありませんので、（許容誤差の程度にもよりますが）距離の逆 2 乗則を“そのまま”適用することができない場合も多くあると考えた方がよいでしょう。つまり、光源の大きさが距離に比べて相対的に大きくなればなるほど、距離を離してもそれほど暗くならないということになります。
ただ、或る大きさを持つ光源（面光源など）の場合でも、その光源を多数の小区画（ S1 、S2 、S3 、・・・）に分割して考えれば、それぞれの小区画はほぼ点光源と見做すことができます。従って、個々の小区画から放たれる光束
（φ1 、φ2 、φ3 、・・・）に対しては照度に関する距離の逆 2 乗則を個別に適用することができます。対向する面上の小区画（単位面積 A ）の照度は、これらが同時に重なって入射した結果、すなわち
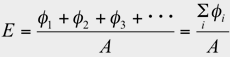
ですので、この関係から、面光源の場合でも理論的積分計算によって照度を求めることが可能になります。（実際には、距離の逆 2 乗則と斜入射光特性の組合せの計算になります。）
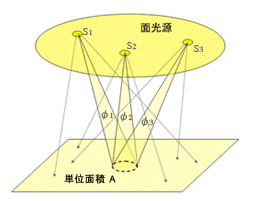
≪※4≫ 日本（北半球）では夏が暑くて冬が寒い理由
日本（北半球）では夏が暑くて冬が寒いのは、照度の斜入射光特性（コサイン特性）のためと言えます。地球は太陽の周りを 1 年かけて公転していますが、太陽と地球の距離は約 1 億 5000 万 km で季節によって大きな変化はありません。地球の回転軸（地軸）は公転面の法線に対して 23.5° 傾いていますので、地球が公転軌道上で正反対の位置にある夏と冬では地表に対する太陽光の入射角度が異なります。夏は入射角が小さく（地表から見れば太陽の高さが高く）、冬は入射角が大きく（地表から見れば太陽の高さが低く）なります。つまり、夏は照度が高くなるため温まり易く、冬は照度が低くなるため温まりにくい、ということになります。 （実際の暑さ、寒さのピークが夏至あるいは冬至から 2 ヶ月くらいずれるのは、地球の比熱のため時間遅れが発生するからです。）
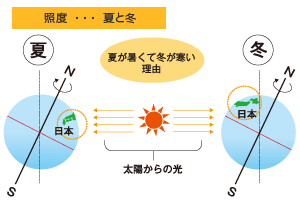
≪※5≫ コサイン4乗則
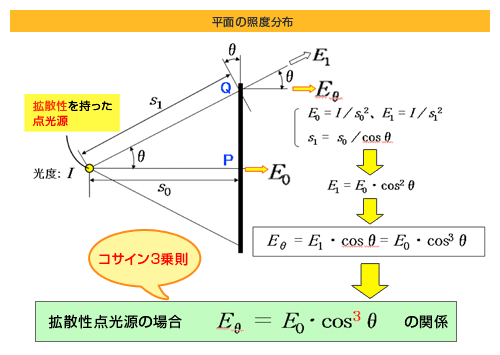
先ず、四方八方に均等に光を放出する点光源（光度 I ）により、距離 s0 にある平面を照明する場合を考えます。垂直入射点 P の照度 E0 は距離の逆 2 乗則により
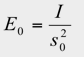
となります。次に、点光源から斜め θ 方向の平面上の点 Q の照度を計算します。点光源から点 Q までの距離を s1 とし、点 Q を通り光源の正対する仮想の平面を考え、この仮想平面上の照度を E1 とします。
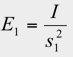であり、また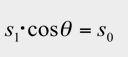 
の関係がありますので、仮想平面上の照度 E1 は
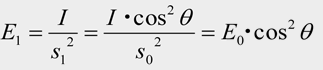
となります。この仮想平面は、実際の平面に対して角度 θ だけ傾いていますので、実際の平面への入射角 は θ となり、点 Q の照度は更に cosθ のファクタが掛かることになり、結局、点 Q の照度 Eθ は
Eθ = E1・cosθ = ( E0・cos2 θ )・cosθ = E0・cos3 θ
となります。
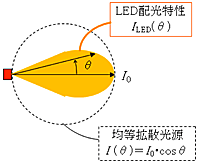
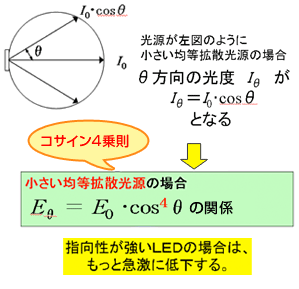
以上は、四方八方全方向へ均等な光度 I を持つ拡散性点光源の場合ですが、実際の光源の場合はある面積を持っており、“或る方向に向かって”光っている場合が殆どです。その典型的配光特性として、「均等拡散面（ Lambertian ）」と呼ばれる特性を考えてみます。「均等拡散面」は、どの方向から見ても輝度が変わらない光源面（または反射面）で、照明工学における光源面（あるは反射面）の基準特性です。詳しくは、次回の「輝度の性質」で説明予定です。
均等拡散光源の配光特性は、正面（ 0° ）方向への光度を I0 としたとき、θ 方向の光度Iθ が
Iθ = I0・cosθ
と定義されます。従って、均等拡散性微小面光源で平面を照明した場合の、θ 方向の面上の照度は、上記に更に cosθ が乗じられて、
Eθ = E0・cos4 θ
という理論式が導かれることになります。
光と色の話 第一部
第8回 照度の性質
「照度」の距離依存性と入射角依存性について
はじめに
「照度」は、着目した面の“照らされ度合い”のことでしたね。正確に言えば、光が入射する面の単位面積当りの光束、ということになります。各種測光量の中で、照度は我々の身の回りの照明にとって特に重要で、馴染みの深いものです。また、マシンビジョンにおいても、ワークを照明する条件として重要です。今回は、照度の重要な特性である、距離依存性と入射角依存性についてお話します。
照度と距離の関係 ・・・・・ 照度に関する距離の逆2乗則
我々の生活体験から、その面を照らす光源が遠くなれば、その面の明るさは暗くなる、ということは誰でも知っています。例えば読み書きをする机上の「明るさ」は電気スタンドが近い方が明るくなりますね。
「照度」に関する重要な特性として、光源の大きさが十分小さい（点光源と見做せる）場合、その面の照度は光源からの距離の 2 乗に反比例する、という法則があります。具体的にもう少し詳しく考えて行きましょう。
今、四方八方に均等に光を放出する充分小さい光源（点光源）を想定します。この点光源からは放射状に光が発散放出されています。この点光源から或る立体角範囲に放出される光束は放射状に広がりながら進行していきますので、その光束が照らす「面積」は距離比の 2 乗に比例することになります。つまり距離が遠くなる程、同じ光束でより広い（距離の 2 乗倍の）面積を照明することになりますので、結局、照度すなわち単位面積当りの光束は距離比の 2 乗分の 1 になってしまう訳です。
数式で書くと分かりにくくなってしまいますが、距離が 2 倍になれば照度は 1 / 22 = 1 / 4 に、距離が 3 倍になれば照度は
1 / 32 = 1 / 9 になり、逆に距離が 1 / 2 になれば照度は 22 = 4 倍に、距離が 1 / 3 になれば照度は 32 = 9 倍 になる、と考えれば分かり易いと思います。これが照度に関する距離の逆 2 乗則です。
この法則を適用して、太陽系の各惑星上での真昼の明るさを概略計算してみた結果を≪※1≫に示します。 この法則が成り立つのは、勿論理想的な場合、すなわち「拡散性（四方八方に均等に光を発散している）」の「点光源」の場合≪※2≫であって、実際の光源の場合には光源の大きさがあり、光の放射方向によって強さが異なる場合も多いため、厳密には理想通りにはならず、この理論式からの誤差が出てきます≪※3≫。通常の発散性の光源の場合、大雑把に言って、光源の大きさ（径）に対してその 10 倍以上の距離であれば概ねこの法則（照度に関する距離の逆 2 乗則）が成り立つと考えても良いでしょう。
照度と入射角との関係 ・・・・・ 照度のコサイン特性
光源から或る距離にある面を照明したときの照度は、その面を光の進行方向に垂直にした時が最も明るくなり、その面を傾けると暗くなりますね。照度はその面に入射する光の入射角 θ の余弦（ cos θ ）に比例して変化する、という重要な性質があります。
これを照度の斜入射光特性（コサイン特性）と呼んでいます。
今、円柱状の平行光（光束 φ1 ）が照射面に垂直に入射している場合を考えます。この時の面上の照射面積を A1 、照度を E1 としますと、照度の定義より
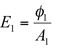
と書けます。一方、この平行光を照射面に斜め方向（入射角 θ ）から入射させた場合を考えます。この時の面上の照射面積を A2 、照度を E2 とします。（光束は変化しませんから φ2 ＝ φ1 です。）斜め方向から照射した場合は、照射面が円柱を斜めに切断する形になりますから
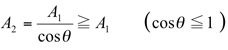
すなわち、垂直入射のときより広い面積を同じ光束（ φ2 ＝ φ1 ）で照明していることになりますから、照度は垂直方向から照明した時より低くなります。 具体的には、斜め方向から照明した時の照度 E2 は、上記の幾何学的な関係から理論的に、
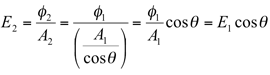
ということになります。
つまり、斜め θ 方向から照明した時の照度（ E2 ）は、垂直方向から照明した時の照度（ E1 ）の cosθ 倍になる、という重要な性質が導かれました。これを図示すると下のグラフのようになります。夏が暑く冬が寒い理由も、この「斜入射光特性（コサイン特性）」の結果として説明されます。≪※4≫
微小面光源による被照明平面の照度分布 ・・・・・ コサイン 4 乗則
上記の、照度に関する「距離の逆 2 乗則」と「斜入射光特性（コサイン特性）」から、照明光学系としての重要な特性である、「コサイン 4 乗則」が導かれます。 「コサイン 4 乗則」とは、拡散性の微小面光源で対向する平面を照明した場合、光源から垂直な対向面の照度(直下照度 E0 ) に対して、角度 θ 方向の面上の照度
( Eθ ) は、cos4θ 倍になる、というものです。数式で書けば
Eθ = E0・cos4 θ
となります。≪※5≫
これは、平面を照明する場合の照度分布を見積る場合の指針となる重要な関係式です。 直下（ 0° 方向）の照度に比べて、周辺へ行くほど照度が急激に低下することを示しています。 例えば、 30° 方向の平面上の照度はおよそ半分強に、 45° 方向の照度は 4 分の 1 になってしまいます。 実際の光源の場合は、一言で拡散性と言っても、その配光特性は様々であり、この理論通りになるとは限りませんが、大雑把な傾向を示す目安として知っておくと便利です。
LED 照明などの場合には、配光特性が拡散性とは言い切れない（指向性が強い）場合も多くあり、そのような場合には cos4θ よりももっと急激に照度が低下し、半ばスポット照明のような照度分布になってしまう場合もあります。
今回の照度の性質は、分光的条件には無関係で、幾何学的条件によって決まりますので、放射照度（センサー照度）に対しても全く共通しています。
注釈
≪※1≫ 冥王星での真昼の明るさはどのくらい?
具体的な例を挙げて大雑把な計算をしてみましょう。我々の地球は太陽からの光を受けて昼夜の明るさを得ていますね。地表の照度は、地球上の位置（緯度）や時刻、天候などの状況によって色々ですが、日本の真夏の晴天真昼間の最大照度は十数万 lx 程度と言われています。仮に 10 万 lx とした場合、この条件下で、他の惑星ではどのくらいの照度になっているのでしょうか?
当然惑星表面の照度はその惑星を取り巻く大気や天候や諸々の条件によって変わると思われますが、それらは一切無視して、大気層も無いものと仮定して計算してみましょう。
太陽から地球までの距離はおよそ 1 億 5000 万 km で、 10 万 lx の照度になっています。太陽から火星までの距離はおよそ 2 億 2300 万 km ということですので地球の場合との距離比は約 1.5 倍、従って火星では照度が
10 万 lx × 1 / 1.52 ≒ 4 万 5000 lx 位となります。 同様にして、太陽・土星間の距離はおよそ 15 億 km、太陽・冥王星間の距離はおよそ 60 億 km とのことですので、地球の場合との距離比はそれぞれ 10 倍、および 40 倍になります。従って、照度はそれぞれ地球の照度（ 10 万 lx ）の 1 / 102 ＝ 1 / 100 および
1 / 402 = 1 / 1600 、すなわち、 1000 lx および 60 lx という計算になります。
つまり、地球上で真夏のカンカン照りで 10 万 lx の照度のときでも、冥王星では 60 lx 程度、すなわち、通常の作業机の下の空間くらいの薄暗さになっているという感じですね。 （なお、冥王星は 1930 年に発見されて以来、太陽系の第 9 惑星とされていましたが、 2006 年に国際天文学連合総会で準惑星という位置付けに変更されました。）
≪※2≫ 照度に関する距離の2乗則の理論的導出
照度に関する距離の逆 2 乗則は、光度、照度、および立体角の定義から理論的に導き出されます。
光度Iの定義は、単位立体角当りの光束で
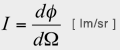
照度の定義は、単位面積当りの光束で、
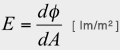
立体角の定義は、球面上の単位面積を球の半径の 2 乗で割ったもので、
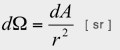
でした。従って、これらの 3 つの定義式から
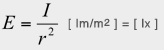
すなわち、照度は光度に比例し、距離の 2 乗に逆比例する、という理論式が導かれます。 ただし、拡散性点光源（光源の面積が無限小）であることがこの法則の前提条件です。
≪※3≫ 照度に関する距離の逆 2 乗則の誤差
照度に関する距離の逆 2 乗則は、厳密には四方八方に均等に光を発散している「点光源」に対して理論的に成立する法則です。実際の光源は当然「点光源」ではなく、ある大きさを持っていますし、配光特性も全方向に対して均等という訳ではありませんので、（許容誤差の程度にもよりますが）距離の逆 2 乗則を“そのまま”適用することができない場合も多くあると考えた方がよいでしょう。つまり、光源の大きさが距離に比べて相対的に大きくなればなるほど、距離を離してもそれほど暗くならないということになります。
ただ、或る大きさを持つ光源（面光源など）の場合でも、その光源を多数の小区画（ S1 、S2 、S3 、・・・）に分割して考えれば、それぞれの小区画はほぼ点光源と見做すことができます。従って、個々の小区画から放たれる光束
（φ1 、φ2 、φ3 、・・・）に対しては照度に関する距離の逆 2 乗則を個別に適用することができます。対向する面上の小区画（単位面積 A ）の照度は、これらが同時に重なって入射した結果、すなわち
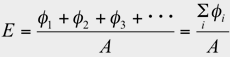
ですので、この関係から、面光源の場合でも理論的積分計算によって照度を求めることが可能になります。（実際には、距離の逆 2 乗則と斜入射光特性の組合せの計算になります。）
≪※4≫ 日本（北半球）では夏が暑くて冬が寒い理由
日本（北半球）では夏が暑くて冬が寒いのは、照度の斜入射光特性（コサイン特性）のためと言えます。地球は太陽の周りを 1 年かけて公転していますが、太陽と地球の距離は約 1 億 5000 万 km で季節によって大きな変化はありません。地球の回転軸（地軸）は公転面の法線に対して 23.5° 傾いていますので、地球が公転軌道上で正反対の位置にある夏と冬では地表に対する太陽光の入射角度が異なります。夏は入射角が小さく（地表から見れば太陽の高さが高く）、冬は入射角が大きく（地表から見れば太陽の高さが低く）なります。つまり、夏は照度が高くなるため温まり易く、冬は照度が低くなるため温まりにくい、ということになります。 （実際の暑さ、寒さのピークが夏至あるいは冬至から 2 ヶ月くらいずれるのは、地球の比熱のため時間遅れが発生するからです。）
≪※5≫ コサイン4乗則
先ず、四方八方に均等に光を放出する点光源（光度 I ）により、距離 s0 にある平面を照明する場合を考えます。垂直入射点 P の照度 E0 は距離の逆 2 乗則により
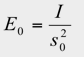
となります。次に、点光源から斜め θ 方向の平面上の点 Q の照度を計算します。点光源から点 Q までの距離を s1 とし、点 Q を通り光源の正対する仮想の平面を考え、この仮想平面上の照度を E1 とします。
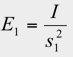であり、また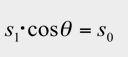
の関係がありますので、仮想平面上の照度 E1 は
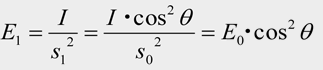
となります。この仮想平面は、実際の平面に対して角度 θ だけ傾いていますので、実際の平面への入射角 は θ となり、点 Q の照度は更に cosθ のファクタが掛かることになり、結局、点 Q の照度 Eθ は
Eθ = E1・cosθ = ( E0・cos2 θ )・cosθ = E0・cos3 θ
となります。
以上は、四方八方全方向へ均等な光度 I を持つ拡散性点光源の場合ですが、実際の光源の場合はある面積を持っており、“或る方向に向かって”光っている場合が殆どです。その典型的配光特性として、「均等拡散面（ Lambertian ）」と呼ばれる特性を考えてみます。「均等拡散面」は、どの方向から見ても輝度が変わらない光源面（または反射面）で、照明工学における光源面（あるは反射面）の基準特性です。詳しくは、次回の「輝度の性質」で説明予定です。
均等拡散光源の配光特性は、正面（ 0° ）方向への光度を I0 としたとき、θ 方向の光度Iθ が
Iθ = I0・cosθ
と定義されます。従って、均等拡散性微小面光源で平面を照明した場合の、θ 方向の面上の照度は、上記に更に cosθ が乗じられて、
Eθ = E0・cos4 θ
という理論式が導かれることになります。
光と色の話 第一部
第8回 照度の性質
「照度」の距離依存性と入射角依存性について
はじめに
「照度」は、着目した面の“照らされ度合い”のことでしたね。正確に言えば、光が入射する面の単位面積当りの光束、ということになります。各種測光量の中で、照度は我々の身の回りの照明にとって特に重要で、馴染みの深いものです。また、マシンビジョンにおいても、ワークを照明する条件として重要です。今回は、照度の重要な特性である、距離依存性と入射角依存性についてお話します。
照度と距離の関係 ・・・・・ 照度に関する距離の逆2乗則
我々の生活体験から、その面を照らす光源が遠くなれば、その面の明るさは暗くなる、ということは誰でも知っています。例えば読み書きをする机上の「明るさ」は電気スタンドが近い方が明るくなりますね。
「照度」に関する重要な特性として、光源の大きさが十分小さい（点光源と見做せる）場合、その面の照度は光源からの距離の 2 乗に反比例する、という法則があります。具体的にもう少し詳しく考えて行きましょう。
今、四方八方に均等に光を放出する充分小さい光源（点光源）を想定します。この点光源からは放射状に光が発散放出されています。この点光源から或る立体角範囲に放出される光束は放射状に広がりながら進行していきますので、その光束が照らす「面積」は距離比の 2 乗に比例することになります。つまり距離が遠くなる程、同じ光束でより広い（距離の 2 乗倍の）面積を照明することになりますので、結局、照度すなわち単位面積当りの光束は距離比の 2 乗分の 1 になってしまう訳です。
数式で書くと分かりにくくなってしまいますが、距離が 2 倍になれば照度は 1 / 22 = 1 / 4 に、距離が 3 倍になれば照度は
1 / 32 = 1 / 9 になり、逆に距離が 1 / 2 になれば照度は 22 = 4 倍に、距離が 1 / 3 になれば照度は 32 = 9 倍 になる、と考えれば分かり易いと思います。これが照度に関する距離の逆 2 乗則です。
この法則を適用して、太陽系の各惑星上での真昼の明るさを概略計算してみた結果を≪※1≫に示します。 この法則が成り立つのは、勿論理想的な場合、すなわち「拡散性（四方八方に均等に光を発散している）」の「点光源」の場合≪※2≫であって、実際の光源の場合には光源の大きさがあり、光の放射方向によって強さが異なる場合も多いため、厳密には理想通りにはならず、この理論式からの誤差が出てきます≪※3≫。通常の発散性の光源の場合、大雑把に言って、光源の大きさ（径）に対してその 10 倍以上の距離であれば概ねこの法則（照度に関する距離の逆 2 乗則）が成り立つと考えても良いでしょう。
照度と入射角との関係 ・・・・・ 照度のコサイン特性
光源から或る距離にある面を照明したときの照度は、その面を光の進行方向に垂直にした時が最も明るくなり、その面を傾けると暗くなりますね。照度はその面に入射する光の入射角 θ の余弦（ cos θ ）に比例して変化する、という重要な性質があります。
これを照度の斜入射光特性（コサイン特性）と呼んでいます。
今、円柱状の平行光（光束 φ1 ）が照射面に垂直に入射している場合を考えます。この時の面上の照射面積を A1 、照度を E1 としますと、照度の定義より
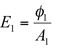
と書けます。一方、この平行光を照射面に斜め方向（入射角 θ ）から入射させた場合を考えます。この時の面上の照射面積を A2 、照度を E2 とします。（光束は変化しませんから φ2 ＝ φ1 です。）斜め方向から照射した場合は、照射面が円柱を斜めに切断する形になりますから
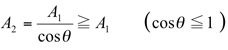
すなわち、垂直入射のときより広い面積を同じ光束（ φ2 ＝ φ1 ）で照明していることになりますから、照度は垂直方向から照明した時より低くなります。 具体的には、斜め方向から照明した時の照度 E2 は、上記の幾何学的な関係から理論的に、
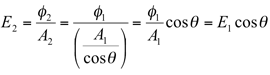
ということになります。
つまり、斜め θ 方向から照明した時の照度（ E2 ）は、垂直方向から照明した時の照度（ E1 ）の cosθ 倍になる、という重要な性質が導かれました。これを図示すると下のグラフのようになります。夏が暑く冬が寒い理由も、この「斜入射光特性（コサイン特性）」の結果として説明されます。≪※4≫
微小面光源による被照明平面の照度分布 ・・・・・ コサイン 4 乗則
上記の、照度に関する「距離の逆 2 乗則」と「斜入射光特性（コサイン特性）」から、照明光学系としての重要な特性である、「コサイン 4 乗則」が導かれます。 「コサイン 4 乗則」とは、拡散性の微小面光源で対向する平面を照明した場合、光源から垂直な対向面の照度(直下照度 E0 ) に対して、角度 θ 方向の面上の照度
( Eθ ) は、cos4θ 倍になる、というものです。数式で書けば
Eθ = E0・cos4 θ
となります。≪※5≫
これは、平面を照明する場合の照度分布を見積る場合の指針となる重要な関係式です。 直下（ 0° 方向）の照度に比べて、周辺へ行くほど照度が急激に低下することを示しています。 例えば、 30° 方向の平面上の照度はおよそ半分強に、 45° 方向の照度は 4 分の 1 になってしまいます。 実際の光源の場合は、一言で拡散性と言っても、その配光特性は様々であり、この理論通りになるとは限りませんが、大雑把な傾向を示す目安として知っておくと便利です。
LED 照明などの場合には、配光特性が拡散性とは言い切れない（指向性が強い）場合も多くあり、そのような場合には cos4θ よりももっと急激に照度が低下し、半ばスポット照明のような照度分布になってしまう場合もあります。
今回の照度の性質は、分光的条件には無関係で、幾何学的条件によって決まりますので、放射照度（センサー照度）に対しても全く共通しています。
注釈
≪※1≫ 冥王星での真昼の明るさはどのくらい?
具体的な例を挙げて大雑把な計算をしてみましょう。我々の地球は太陽からの光を受けて昼夜の明るさを得ていますね。地表の照度は、地球上の位置（緯度）や時刻、天候などの状況によって色々ですが、日本の真夏の晴天真昼間の最大照度は十数万 lx 程度と言われています。仮に 10 万 lx とした場合、この条件下で、他の惑星ではどのくらいの照度になっているのでしょうか?
当然惑星表面の照度はその惑星を取り巻く大気や天候や諸々の条件によって変わると思われますが、それらは一切無視して、大気層も無いものと仮定して計算してみましょう。
太陽から地球までの距離はおよそ 1 億 5000 万 km で、 10 万 lx の照度になっています。太陽から火星までの距離はおよそ 2 億 2300 万 km ということですので地球の場合との距離比は約 1.5 倍、従って火星では照度が
10 万 lx × 1 / 1.52 ≒ 4 万 5000 lx 位となります。 同様にして、太陽・土星間の距離はおよそ 15 億 km、太陽・冥王星間の距離はおよそ 60 億 km とのことですので、地球の場合との距離比はそれぞれ 10 倍、および 40 倍になります。従って、照度はそれぞれ地球の照度（ 10 万 lx ）の 1 / 102 ＝ 1 / 100 および
1 / 402 = 1 / 1600 、すなわち、 1000 lx および 60 lx という計算になります。
つまり、地球上で真夏のカンカン照りで 10 万 lx の照度のときでも、冥王星では 60 lx 程度、すなわち、通常の作業机の下の空間くらいの薄暗さになっているという感じですね。 （なお、冥王星は 1930 年に発見されて以来、太陽系の第 9 惑星とされていましたが、 2006 年に国際天文学連合総会で準惑星という位置付けに変更されました。）
≪※2≫ 照度に関する距離の2乗則の理論的導出
照度に関する距離の逆 2 乗則は、光度、照度、および立体角の定義から理論的に導き出されます。
光度Iの定義は、単位立体角当りの光束で
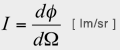
照度の定義は、単位面積当りの光束で、
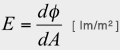
立体角の定義は、球面上の単位面積を球の半径の 2 乗で割ったもので、
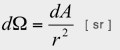
でした。従って、これらの 3 つの定義式から
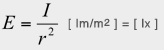
すなわち、照度は光度に比例し、距離の 2 乗に逆比例する、という理論式が導かれます。 ただし、拡散性点光源（光源の面積が無限小）であることがこの法則の前提条件です。
≪※3≫ 照度に関する距離の逆 2 乗則の誤差
照度に関する距離の逆 2 乗則は、厳密には四方八方に均等に光を発散している「点光源」に対して理論的に成立する法則です。実際の光源は当然「点光源」ではなく、ある大きさを持っていますし、配光特性も全方向に対して均等という訳ではありませんので、（許容誤差の程度にもよりますが）距離の逆 2 乗則を“そのまま”適用することができない場合も多くあると考えた方がよいでしょう。つまり、光源の大きさが距離に比べて相対的に大きくなればなるほど、距離を離してもそれほど暗くならないということになります。
ただ、或る大きさを持つ光源（面光源など）の場合でも、その光源を多数の小区画（ S1 、S2 、S3 、・・・）に分割して考えれば、それぞれの小区画はほぼ点光源と見做すことができます。従って、個々の小区画から放たれる光束
（φ1 、φ2 、φ3 、・・・）に対しては照度に関する距離の逆 2 乗則を個別に適用することができます。対向する面上の小区画（単位面積 A ）の照度は、これらが同時に重なって入射した結果、すなわち
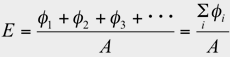
ですので、この関係から、面光源の場合でも理論的積分計算によって照度を求めることが可能になります。（実際には、距離の逆 2 乗則と斜入射光特性の組合せの計算になります。）
≪※4≫ 日本（北半球）では夏が暑くて冬が寒い理由
日本（北半球）では夏が暑くて冬が寒いのは、照度の斜入射光特性（コサイン特性）のためと言えます。地球は太陽の周りを 1 年かけて公転していますが、太陽と地球の距離は約 1 億 5000 万 km で季節によって大きな変化はありません。地球の回転軸（地軸）は公転面の法線に対して 23.5° 傾いていますので、地球が公転軌道上で正反対の位置にある夏と冬では地表に対する太陽光の入射角度が異なります。夏は入射角が小さく（地表から見れば太陽の高さが高く）、冬は入射角が大きく（地表から見れば太陽の高さが低く）なります。つまり、夏は照度が高くなるため温まり易く、冬は照度が低くなるため温まりにくい、ということになります。 （実際の暑さ、寒さのピークが夏至あるいは冬至から 2 ヶ月くらいずれるのは、地球の比熱のため時間遅れが発生するからです。）
≪※5≫ コサイン4乗則
先ず、四方八方に均等に光を放出する点光源（光度 I ）により、距離 s0 にある平面を照明する場合を考えます。垂直入射点 P の照度 E0 は距離の逆 2 乗則により
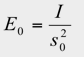
となります。次に、点光源から斜め θ 方向の平面上の点 Q の照度を計算します。点光源から点 Q までの距離を s1 とし、点 Q を通り光源の正対する仮想の平面を考え、この仮想平面上の照度を E1 とします。
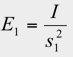であり、また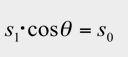
の関係がありますので、仮想平面上の照度 E1 は
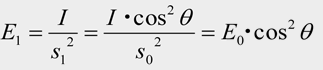
となります。この仮想平面は、実際の平面に対して角度 θ だけ傾いていますので、実際の平面への入射角 は θ となり、点 Q の照度は更に cosθ のファクタが掛かることになり、結局、点 Q の照度 Eθ は
Eθ = E1・cosθ = ( E0・cos2 θ )・cosθ = E0・cos3 θ
となります。
以上は、四方八方全方向へ均等な光度 I を持つ拡散性点光源の場合ですが、実際の光源の場合はある面積を持っており、“或る方向に向かって”光っている場合が殆どです。その典型的配光特性として、「均等拡散面（ Lambertian ）」と呼ばれる特性を考えてみます。「均等拡散面」は、どの方向から見ても輝度が変わらない光源面（または反射面）で、照明工学における光源面（あるは反射面）の基準特性です。詳しくは、次回の「輝度の性質」で説明予定です。
均等拡散光源の配光特性は、正面（ 0° ）方向への光度を I0 としたとき、θ 方向の光度Iθ が
Iθ = I0・cosθ
と定義されます。従って、均等拡散性微小面光源で平面を照明した場合の、θ 方向の面上の照度は、上記に更に cosθ が乗じられて、
Eθ = E0・cos4 θ
という理論式が導かれることになります。