光と色の話 第一部

第30回 色の客観的な表現と伝達 (その4)
・・・・・ CIE - RGB 表色系から XYZ 表色系へ ・・・・・
光の三原色の加法混色
本連載の第 16 回、17 回でお話しましたように、加法混色(同時加法混色)では、三原色の赤、緑、青の色光を混ぜ合わすことによって、様々な色を作り出すことができます。つまり、この時の三原色の混色比を指定すれば混色結果の色が一義的に決まることになりますので、これに基いて表色系の構成が可能になる訳です。
等色実験
1931 年 CIE(国際照明委員会)で採択された XYZ 表色系では以下のような「等色実験」と呼ばれる基礎実験結果を元に表色系が組み立てられました。色光の 3 原色[ R ]、[ G ]、[ B ]として
[ R ] : λ R = 700.0 nm
[ G ] : λ G = 546.1 nm
[ B ] : λ B = 435.8 nm
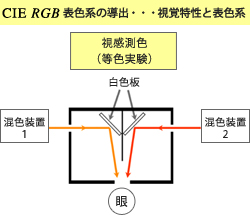
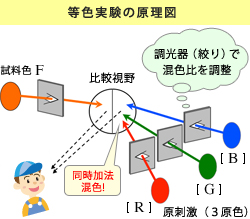
の 3 種の波長の単色光≪※1≫を採用し、これらの三原色を加法混色した結果と、様々な波長の単色光の色とを比較し、同じ色に見える(これを「等色する」と言います)混色比を求める実験を行った訳です。実験装置は右上図のような原理的構成になっています。
直交配置させた拡散性の良い 2 枚の白色板の表面の色を、覗き穴から左右の視野として肉眼で観察するようになっています。この 2 枚の白色反射板には、左右の孔から別々の色光を入射させ、白色板表面で拡散反射された光色を左右の視野で同時に比較し、両視野の色が同じに見えるかどうかを判断する訳です。
今、例えば左側の入射孔から或る波長 λ の試料単色光(この光の色を F と表します) を入射させ、右側の入射孔から赤、緑、青の三原色
[ R ]、[ G ]、[ B ]を加法混色させた色光を入射させ、左右の白色板からの反射光の色を比較します。
右視野の混色光は 三原色[ R ]、[ G ]、[ B ]を r : g : b の混色比で加法混色したもので、
r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。
従って、調光器(絞りなど)で三原色の混色比 r : g : b を色々変えながら調整し、左右の視野が 「等色」 した時には
F ≡ r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。記号 「 ≡ 」 は、色彩学では「等色記号」と言い、「同じ色に見える」という意味です。
RGB 表色系の等色関数
このような等色実験を、左側から入射させる単色光 F の波長 λ を変えながら、それぞれの波長毎に、等色する混色比 r : g : b を求める実験を繰り返します。(等色実験では、このように試料単色光の波長 λ を変数として扱いますので、
以下の記述は関数形式 F ( λ ) 、r ( λ ) 、g ( λ ) 、b ( λ ) で表記します。)
その結果得られた波長毎の混色比特性が RGB 表色系の等色関数と言われるものです(右図)≪※2≫ 。
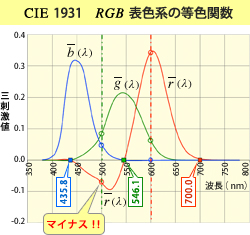
例えば、波長 λ = 600 nm の単色光 F ( 600 ) に対しては、[ R ]、[ G ]、[ B ]をそれぞれ
r ( λ ) = 0.3443 、 g ( λ ) = 0.0624、 b ( λ ) = 0.0005
の比率で混色すれば等色することを示しています。
ところで、この図を見ると、等色関数の値がマイナスになっている波長域があることに気がつきますね。( r ( λ ) の 435.8 ~ 546.1 nm の波長域が特に目立ちます。≪※3≫ )
等色するための混色比を示す値がマイナスというのは一体どういうことなのでしょうか?
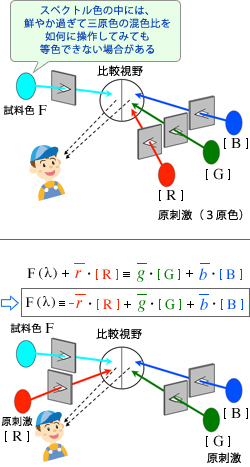
これは、この波長域の単色光の色 F ( λ ) に対しては、実在の三原色[ R ]、
[ G ]、[ B ]の混色比をどのように変えてみても、単色光 F ( λ ) の方が鮮やか過ぎて等色できないことを示しています。このように如何にしても等色できない場合、三原色の内のどれかを試料光 F ( λ ) 側へ移動させて試料光と混色させるという操作をしてやれば、右側視野の残りの二原色の混色と等色できる条件を作り出すことができます。
例えば、(青緑色に見える)波長 λ = 500 nm の単色光 F ( 500 ) の場合、これに原色の赤[ R ]を r ( λ ) = 0.072 だけ混色し、 更に右視野の緑[ G ]と
青[ B ]を g ( λ ) = 0.085、b ( λ ) = 0.048 という比率で混色すれば、両視野の色が一致しますので、
F ( λ ) + r ( λ )・[ R ]≡ g ( λ )・[ G ]+ b ( λ )・[ B ]
という等色式が得られます。この等色式の r ( λ )・[ R ]を右辺に移項してやれば
F ( λ ) ≡- r ( λ )・[ R ]+ g ( λ )・[ G ]+ b ( λ )・[ B ]
となります。
これが、 波長 λ = 500 nm で等色関数 r ( λ ) がマイナス表記される理由です。
RGB 表色系の色度図 ( r g 色度図)
このようにして得られた等色関数 r ( λ ) 、 g ( λ ) 、 b ( λ ) によって、三原色 [ R ]、[ G ]、[ B ]による刺激値 R 、G 、B が定義されます( k は定数 )。
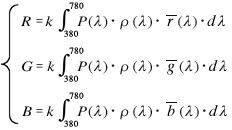
これより
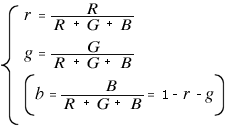
とすると、r は全刺激量に対する赤の刺激量の比、g は全刺激量に対する緑の刺激量の比、b は全刺激量に対する青の刺激量の比を示します。ここで、r を横軸に、g を縦軸にとって色度図を描くと下図のようになり、これを r g 色度図と言います≪※4≫。
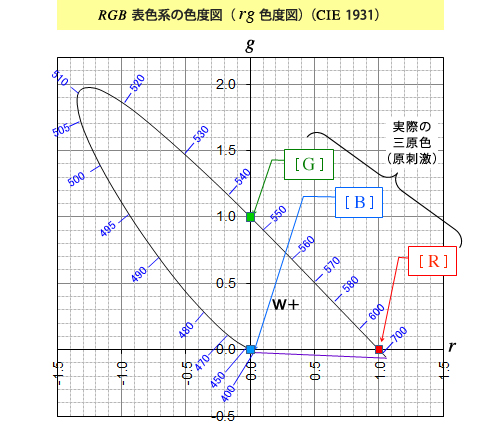
この r g 色度図の曲線部分は単色光軌跡(またはスペクトル軌跡)と呼ばれ、図中に示した数値はその座標位置に対応する単色光の波長を示しています。また、単色光軌跡の曲線両端(可視域の両端の単色光の色度点)を結ぶ直線を純紫軌跡と呼びます。純紫軌跡上には単色光の色度点は存在せず、可視域両端の単色光の加法混色の結果として得られる色の色度点として得られるものです。
世の中のすべての色は、この曲線(単色光軌跡)と直線(純紫軌跡)で囲まれた領域内の色度点で表され、例えば、三原色を均等に混色してできる無彩色はW+で示した位置
( r , g )= ( 0.333 , 0.333 )
になります。
r g 色度図を見ると、第2象限( r < 0 、g > 0 ) の領域に色度域が大きく張り出しているのが目立ちます。この領域は
r < 0 すなわち R < 0 ですから、上述のように、実在する三原色 [ R ]、[ G ]、[ B ]の加法混色では作り出せない色・・・・・その色に赤原色 [ R ] を混色すれば、緑原色 [ G ] と青原色 [ B ] を混色した色と等色できる色・・・・・を示す領域です。
このように、RGB 表色系は、等色関数が負の値になる(混色比が負になる)波長域があって直感的に分かりにくく、また、負の刺激量が混在するということは(1931年当時は今のような計算器も無かったこともあって)計算が結構煩雑という問題がありました。
そこで、等色関数がすべて非負(マイナスの値とならない)となるような仮想の原刺激[ X ]、[ Y ]、[ Z ] を設定し、この仮想の三原色による XYZ 表色系が作られました。
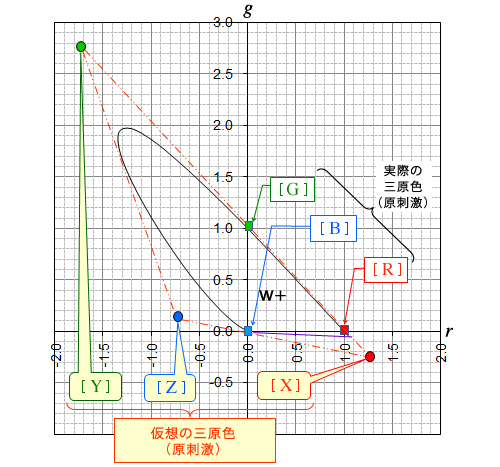
原刺激 [ X ]、[ Y ]、[ Z ] は、上図のような r g 色度図の表色領域に外接する三角形を想定し、その頂点で示される仮想の色(虚色)となります。こうすれば、表色領域の中の全ての座標点は、
[ X ]、[ Y ]、[ Z ] の非負の混色比で表示することが可能になります。
この図の [ Y ] と [ Z ] を結ぶ直線が縦軸に、[ Z ] と[ X ] を結ぶ直線が横軸になるように座標変換してやれば、全ての表色領域が、直交座標の第1象限内で表現することが可能になります。また、更に「明度」に関する条件として
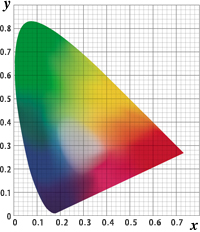
y ( λ ) ≡ V ( λ ) を加えて座標変換して得られた色度図が XYZ 表色系の x y 色度図(右図)です。≪※5≫
三刺激値 X、Y、Z と 視細胞( L 、 M 、 S 錐体)との関係
上述のように座標変換した結果、RGB 表色系の三刺激値 R、G、B と XYZ 表色系の三刺激値 X、Y、Z の間には以下の式で表される関係があります。
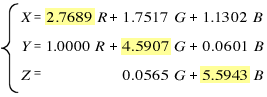
この関係式の、 R、G、B の係数の大きさに注目して下さい。黄色で着色した係数が他の係数に比べて突出して大きいことが分かります。つまりこれは、刺激値 X は R が主成分になって、それに幾分かの G と B の成分が加味されていることを示しています。同様に、刺激値 Y は G が主成分で、R と B が幾分加味されたものであり、刺激値 Z は B が主成分で、G が幾分加味されているということです。これは、XYZ 表色系の等色関数 x ( λ ) 、 y ( λ ) 、 z ( λ ) のグラフと対応させて見ればよくわかるかと思います。別の表現をすれば、刺激値 X は、視細胞の L 錐体の応答が主成分で、それに M 錐体、 S 錐体の応答が加味されたもの、刺激値 Y は M 錐体の応答が主成分でそれに L 錐体と S 錐体の応答が加味されたもの、刺激値 Z は S 錐体の応答が主成分で M 錐体の応答が加味されたものと言うことができます。
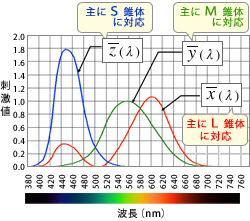
以上のように、CIE 表色系は、人間の視細胞(錐体)の働きに基く色覚特性を科学的実験によって特性づけたデータを基礎にして構築された表色系であると言えます。
注釈
≪※1≫ CIEが設定した単色光三原色の波長
これら三原色の選定については、1931 年当時に比較的容易に利用できた水銀の輝線スペクトルから、
青 ( λ B = 435.8 nm ) と 緑 ( λ G = 546.1 nm ) の原色として、また、赤の原色は、実用上一定以上の色感覚を引き起こす可視域最長のキリのよい波長を選定したようです。
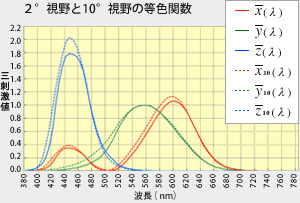
≪※2≫ 等色関数と観察視野角度( 2° 視野 と 10° 視野) ・・・・・ 色の面積効果
試料色の占める面積(視野角の大きさ)によって、ヒトの眼には色の見え方が微妙に異なって見えることが分かっています。これを「色の面積効果」と言っています。これは、網膜上で視細胞(錐体)が集中分布する中心窩部分(ほぼ視野角 2° に相当)のみが黄斑色素で覆われており、黄斑部以外の網膜領域と色覚特性がわずかに異なっていることが原因です。
従って、色を正確に評価するためには、視野角の大きさを規定し、その条件に適した等色関数で評価しなければなりません。1931 年に規定されたのは 2° 視野の等色関数でしたが、その後の運用および研究の結果、もっと大きい視野角(広い試料面積)での評価条件規定が必要であることがわかり、1964 年にその代表条件として 10° 視野の等色関数 x10 ( λ ) 、y10 ( λ ) 、z10 ( λ ) が決められました。本文中で図示した RGB 表色系の等色関数は 2° 視野のものです。なお、視野角が 4° 以下の場合は 2° 視野の等色関数を、4° を超える場合は 10° 視野の等色関数を用いることになっています。
≪※3≫ 負の等色関数
r ( λ ) の 3 つの関数の中で、マイナスの値となるのは r ( λ ) が最も目立ちますが g ( λ ) 、b ( λ ) 、についても、ほんの僅かながらマイナスの値となる波長域が存在します。
≪※4≫ 色度図上での 3 原色の座標
r , g , b の 3 つの変数がありますので、本来は r 軸、g 軸、b 軸の3次元直交座標で表示されるのですが、b の値は r と g の値が決まれば自動的に決まりますから r - g 平面のみで色度を表示できることになります。各原色の座標は対応する軸上の切片 1 の位置に表示されます。
つまり、原色 [ R ] は( r , g )=( 1 , 0 )、原色 [ G ] は( r , g )=( 0 , 1 )となります。
また、原色 [ B ] は b = 1,r =g = 0 ですから、rg 色度図上では原点すなわち ( r , g )=(0 , 0) になります。
≪※5≫ RGB 表色系から XYZ 表色系への座標変換
XYZ 表色系は、RGB 表色系が負の刺激値(負の等色関数)をもつことの解りにくさや不便の解消を主目的としたものですが、更に、もう一つ、「明るさ」を評価する関数である標準分光視感効 V ( λ ) に等色関数の内の y ( λ ) を一致させることを座標変換条件にしたことが大きな特徴として挙げられます。こうすることによって、色の心理的三属性の「色相」と「彩度」の組み合わせを色度座標 ( x , y ) に対応させ、「明度」を刺激値 Y に 対応させた訳です。
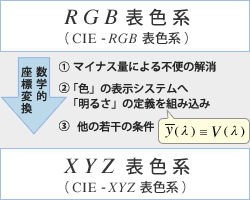
歴史的に見れば、先ず、一次元情報である「明るさ」に対する研究が行われて標準分光視感効率 V ( λ ) が確立され、その後を追うようにして、(色相・彩度・明度の)3 次元情報である色彩の研究が進行しました。その中で、「色彩」を定量表示するシステムを構築する時点で、すでに確立されていた「明るさ」の定量的評価関数である V ( λ ) を取り込んで色の表示システムを構築したというのは、極めて自然な流れであったと言えますね。
光と色の話 第一部

第30回 色の客観的な表現と伝達 (その4)
・・・・・ CIE - RGB 表色系から XYZ 表色系へ ・・・・・
光の三原色の加法混色
本連載の第 16 回、17 回でお話しましたように、加法混色(同時加法混色)では、三原色の赤、緑、青の色光を混ぜ合わすことによって、様々な色を作り出すことができます。つまり、この時の三原色の混色比を指定すれば混色結果の色が一義的に決まることになりますので、これに基いて表色系の構成が可能になる訳です。
等色実験
1931 年 CIE(国際照明委員会)で採択された XYZ 表色系では以下のような「等色実験」と呼ばれる基礎実験結果を元に表色系が組み立てられました。色光の 3 原色[ R ]、[ G ]、[ B ]として
[ R ] : λ R = 700.0 nm
[ G ] : λ G = 546.1 nm
[ B ] : λ B = 435.8 nm
の 3 種の波長の単色光≪※1≫を採用し、これらの三原色を加法混色した結果と、様々な波長の単色光の色とを比較し、同じ色に見える(これを「等色する」と言います)混色比を求める実験を行った訳です。実験装置は右上図のような原理的構成になっています。
直交配置させた拡散性の良い 2 枚の白色板の表面の色を、覗き穴から左右の視野として肉眼で観察するようになっています。この 2 枚の白色反射板には、左右の孔から別々の色光を入射させ、白色板表面で拡散反射された光色を左右の視野で同時に比較し、両視野の色が同じに見えるかどうかを判断する訳です。
今、例えば左側の入射孔から或る波長 λ の試料単色光(この光の色を F と表します) を入射させ、右側の入射孔から赤、緑、青の三原色
[ R ]、[ G ]、[ B ]を加法混色させた色光を入射させ、左右の白色板からの反射光の色を比較します。
右視野の混色光は 三原色[ R ]、[ G ]、[ B ]を r : g : b の混色比で加法混色したもので、
r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。
従って、調光器(絞りなど)で三原色の混色比 r : g : b を色々変えながら調整し、左右の視野が 「等色」 した時には
F ≡ r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。記号 「 ≡ 」 は、色彩学では「等色記号」と言い、「同じ色に見える」という意味です。


RGB 表色系の等色関数
このような等色実験を、左側から入射させる単色光 F の波長 λ を変えながら、それぞれの波長毎に、等色する混色比 r : g : b を求める実験を繰り返します。(等色実験では、このように試料単色光の波長 λ を変数として扱いますので、
以下の記述は関数形式 F ( λ ) 、r ( λ ) 、g ( λ ) 、b ( λ ) で表記します。)
その結果得られた波長毎の混色比特性が RGB 表色系の等色関数と言われるものです(右図)≪※2≫ 。

例えば、波長 λ = 600 nm の単色光 F ( 600 ) に対しては、[ R ]、[ G ]、[ B ]をそれぞれ
r ( λ ) = 0.3443 、 g ( λ ) = 0.0624、 b ( λ ) = 0.0005
の比率で混色すれば等色することを示しています。
ところで、この図を見ると、等色関数の値がマイナスになっている波長域があることに気がつきますね。( r ( λ ) の 435.8 ~ 546.1 nm の波長域が特に目立ちます。≪※3≫ )
等色するための混色比を示す値がマイナスというのは一体どういうことなのでしょうか?
これは、この波長域の単色光の色 F ( λ ) に対しては、実在の三原色[ R ]、
[ G ]、[ B ]の混色比をどのように変えてみても、単色光 F ( λ ) の方が鮮やか過ぎて等色できないことを示しています。このように如何にしても等色できない場合、三原色の内のどれかを試料光 F ( λ ) 側へ移動させて試料光と混色させるという操作をしてやれば、右側視野の残りの二原色の混色と等色できる条件を作り出すことができます。
例えば、(青緑色に見える)波長 λ = 500 nm の単色光 F ( 500 ) の場合、これに原色の赤[ R ]を r ( λ ) = 0.072 だけ混色し、 更に右視野の緑[ G ]と
青[ B ]を g ( λ ) = 0.085、b ( λ ) = 0.048 という比率で混色すれば、両視野の色が一致しますので、
F ( λ ) + r ( λ )・[ R ]≡ g ( λ )・[ G ]+ b ( λ )・[ B ]
という等色式が得られます。この等色式の r ( λ )・[ R ]を右辺に移項してやれば
F ( λ ) ≡- r ( λ )・[ R ]+ g ( λ )・[ G ]+ b ( λ )・[ B ]
となります。
これが、 波長 λ = 500 nm で等色関数 r ( λ ) がマイナス表記される理由です。

RGB 表色系の色度図 ( r g 色度図)
このようにして得られた等色関数 r ( λ ) 、 g ( λ ) 、 b ( λ ) によって、三原色 [ R ]、[ G ]、[ B ]による刺激値 R 、G 、B が定義されます( k は定数 )。
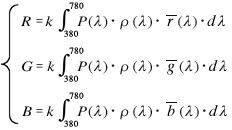
これより
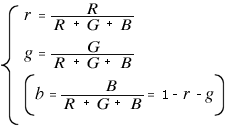
とすると、r は全刺激量に対する赤の刺激量の比、g は全刺激量に対する緑の刺激量の比、b は全刺激量に対する青の刺激量の比を示します。ここで、r を横軸に、g を縦軸にとって色度図を描くと下図のようになり、これを r g 色度図と言います≪※4≫。

この r g 色度図の曲線部分は単色光軌跡(またはスペクトル軌跡)と呼ばれ、図中に示した数値はその座標位置に対応する単色光の波長を示しています。また、単色光軌跡の曲線両端(可視域の両端の単色光の色度点)を結ぶ直線を純紫軌跡と呼びます。純紫軌跡上には単色光の色度点は存在せず、可視域両端の単色光の加法混色の結果として得られる色の色度点として得られるものです。
世の中のすべての色は、この曲線(単色光軌跡)と直線(純紫軌跡)で囲まれた領域内の色度点で表され、例えば、三原色を均等に混色してできる無彩色はW+で示した位置
( r , g )= ( 0.333 , 0.333 )
になります。
r g 色度図を見ると、第2象限( r < 0 、g > 0 ) の領域に色度域が大きく張り出しているのが目立ちます。この領域は
r < 0 すなわち R < 0 ですから、上述のように、実在する三原色 [ R ]、[ G ]、[ B ]の加法混色では作り出せない色・・・・・その色に赤原色 [ R ] を混色すれば、緑原色 [ G ] と青原色 [ B ] を混色した色と等色できる色・・・・・を示す領域です。
このように、RGB 表色系は、等色関数が負の値になる(混色比が負になる)波長域があって直感的に分かりにくく、また、負の刺激量が混在するということは(1931年当時は今のような計算器も無かったこともあって)計算が結構煩雑という問題がありました。
そこで、等色関数がすべて非負(マイナスの値とならない)となるような仮想の原刺激[ X ]、[ Y ]、[ Z ] を設定し、この仮想の三原色による XYZ 表色系が作られました。

原刺激 [ X ]、[ Y ]、[ Z ] は、上図のような r g 色度図の表色領域に外接する三角形を想定し、その頂点で示される仮想の色(虚色)となります。こうすれば、表色領域の中の全ての座標点は、
[ X ]、[ Y ]、[ Z ] の非負の混色比で表示することが可能になります。
この図の [ Y ] と [ Z ] を結ぶ直線が縦軸に、[ Z ] と[ X ] を結ぶ直線が横軸になるように座標変換してやれば、全ての表色領域が、直交座標の第1象限内で表現することが可能になります。また、更に「明度」に関する条件として
y ( λ ) ≡ V ( λ ) を加えて座標変換して得られた色度図が XYZ 表色系の x y 色度図(右図)です。≪※5≫

三刺激値 X、Y、Z と 視細胞( L 、 M 、 S 錐体)との関係
上述のように座標変換した結果、RGB 表色系の三刺激値 R、G、B と XYZ 表色系の三刺激値 X、Y、Z の間には以下の式で表される関係があります。
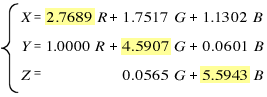
この関係式の、 R、G、B の係数の大きさに注目して下さい。黄色で着色した係数が他の係数に比べて突出して大きいことが分かります。つまりこれは、刺激値 X は R が主成分になって、それに幾分かの G と B の成分が加味されていることを示しています。同様に、刺激値 Y は G が主成分で、R と B が幾分加味されたものであり、刺激値 Z は B が主成分で、G が幾分加味されているということです。これは、XYZ 表色系の等色関数 x ( λ ) 、 y ( λ ) 、 z ( λ ) のグラフと対応させて見ればよくわかるかと思います。別の表現をすれば、刺激値 X は、視細胞の L 錐体の応答が主成分で、それに M 錐体、 S 錐体の応答が加味されたもの、刺激値 Y は M 錐体の応答が主成分でそれに L 錐体と S 錐体の応答が加味されたもの、刺激値 Z は S 錐体の応答が主成分で M 錐体の応答が加味されたものと言うことができます。

以上のように、CIE 表色系は、人間の視細胞(錐体)の働きに基く色覚特性を科学的実験によって特性づけたデータを基礎にして構築された表色系であると言えます。
注釈
≪※1≫ CIEが設定した単色光三原色の波長
これら三原色の選定については、1931 年当時に比較的容易に利用できた水銀の輝線スペクトルから、
青 ( λ B = 435.8 nm ) と 緑 ( λ G = 546.1 nm ) の原色として、また、赤の原色は、実用上一定以上の色感覚を引き起こす可視域最長のキリのよい波長を選定したようです。
≪※2≫ 等色関数と観察視野角度( 2° 視野 と 10° 視野) ・・・・・ 色の面積効果
試料色の占める面積(視野角の大きさ)によって、ヒトの眼には色の見え方が微妙に異なって見えることが分かっています。これを「色の面積効果」と言っています。これは、網膜上で視細胞(錐体)が集中分布する中心窩部分(ほぼ視野角 2° に相当)のみが黄斑色素で覆われており、黄斑部以外の網膜領域と色覚特性がわずかに異なっていることが原因です。
従って、色を正確に評価するためには、視野角の大きさを規定し、その条件に適した等色関数で評価しなければなりません。1931 年に規定されたのは 2° 視野の等色関数でしたが、その後の運用および研究の結果、もっと大きい視野角(広い試料面積)での評価条件規定が必要であることがわかり、1964 年にその代表条件として 10° 視野の等色関数 x10 ( λ ) 、y10 ( λ ) 、z10 ( λ ) が決められました。本文中で図示した RGB 表色系の等色関数は 2° 視野のものです。なお、視野角が 4° 以下の場合は 2° 視野の等色関数を、4° を超える場合は 10° 視野の等色関数を用いることになっています。

≪※3≫ 負の等色関数
r ( λ ) の 3 つの関数の中で、マイナスの値となるのは r ( λ ) が最も目立ちますが g ( λ ) 、b ( λ ) 、についても、ほんの僅かながらマイナスの値となる波長域が存在します。
≪※4≫ 色度図上での 3 原色の座標
r , g , b の 3 つの変数がありますので、本来は r 軸、g 軸、b 軸の3次元直交座標で表示されるのですが、b の値は r と g の値が決まれば自動的に決まりますから r - g 平面のみで色度を表示できることになります。各原色の座標は対応する軸上の切片 1 の位置に表示されます。
つまり、原色 [ R ] は( r , g )=( 1 , 0 )、原色 [ G ] は( r , g )=( 0 , 1 )となります。
また、原色 [ B ] は b = 1,r =g = 0 ですから、rg 色度図上では原点すなわち ( r , g )=(0 , 0) になります。
≪※5≫ RGB 表色系から XYZ 表色系への座標変換
XYZ 表色系は、RGB 表色系が負の刺激値(負の等色関数)をもつことの解りにくさや不便の解消を主目的としたものですが、更に、もう一つ、「明るさ」を評価する関数である標準分光視感効 V ( λ ) に等色関数の内の y ( λ ) を一致させることを座標変換条件にしたことが大きな特徴として挙げられます。こうすることによって、色の心理的三属性の「色相」と「彩度」の組み合わせを色度座標 ( x , y ) に対応させ、「明度」を刺激値 Y に 対応させた訳です。

歴史的に見れば、先ず、一次元情報である「明るさ」に対する研究が行われて標準分光視感効率 V ( λ ) が確立され、その後を追うようにして、(色相・彩度・明度の)3 次元情報である色彩の研究が進行しました。その中で、「色彩」を定量表示するシステムを構築する時点で、すでに確立されていた「明るさ」の定量的評価関数である V ( λ ) を取り込んで色の表示システムを構築したというのは、極めて自然な流れであったと言えますね。
光と色の話 第一部

第30回 色の客観的な表現と伝達 (その4)
・・・・・ CIE - RGB 表色系から XYZ 表色系へ ・・・・・
光の三原色の加法混色
本連載の第 16 回、17 回でお話しましたように、加法混色(同時加法混色)では、三原色の赤、緑、青の色光を混ぜ合わすことによって、様々な色を作り出すことができます。つまり、この時の三原色の混色比を指定すれば混色結果の色が一義的に決まることになりますので、これに基いて表色系の構成が可能になる訳です。
等色実験
1931 年 CIE(国際照明委員会)で採択された XYZ 表色系では以下のような「等色実験」と呼ばれる基礎実験結果を元に表色系が組み立てられました。色光の 3 原色[ R ]、[ G ]、[ B ]として
[ R ] : λ R = 700.0 nm
[ G ] : λ G = 546.1 nm
[ B ] : λ B = 435.8 nm
の 3 種の波長の単色光≪※1≫を採用し、これらの三原色を加法混色した結果と、様々な波長の単色光の色とを比較し、同じ色に見える(これを「等色する」と言います)混色比を求める実験を行った訳です。実験装置は右上図のような原理的構成になっています。
直交配置させた拡散性の良い 2 枚の白色板の表面の色を、覗き穴から左右の視野として肉眼で観察するようになっています。この 2 枚の白色反射板には、左右の孔から別々の色光を入射させ、白色板表面で拡散反射された光色を左右の視野で同時に比較し、両視野の色が同じに見えるかどうかを判断する訳です。
今、例えば左側の入射孔から或る波長 λ の試料単色光(この光の色を F と表します) を入射させ、右側の入射孔から赤、緑、青の三原色
[ R ]、[ G ]、[ B ]を加法混色させた色光を入射させ、左右の白色板からの反射光の色を比較します。
右視野の混色光は 三原色[ R ]、[ G ]、[ B ]を r : g : b の混色比で加法混色したもので、
r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。
従って、調光器(絞りなど)で三原色の混色比 r : g : b を色々変えながら調整し、左右の視野が 「等色」 した時には
F ≡ r・[ R ] + g・[ G ] + b・[ B ]
と表すことができます。記号 「 ≡ 」 は、色彩学では「等色記号」と言い、「同じ色に見える」という意味です。


RGB 表色系の等色関数
このような等色実験を、左側から入射させる単色光 F の波長 λ を変えながら、それぞれの波長毎に、等色する混色比 r : g : b を求める実験を繰り返します。(等色実験では、このように試料単色光の波長 λ を変数として扱いますので、
以下の記述は関数形式 F ( λ ) 、r ( λ ) 、g ( λ ) 、b ( λ ) で表記します。)
その結果得られた波長毎の混色比特性が RGB 表色系の等色関数と言われるものです(右図)≪※2≫ 。

例えば、波長 λ = 600 nm の単色光 F ( 600 ) に対しては、[ R ]、[ G ]、[ B ]をそれぞれ
r ( λ ) = 0.3443 、 g ( λ ) = 0.0624、 b ( λ ) = 0.0005
の比率で混色すれば等色することを示しています。
ところで、この図を見ると、等色関数の値がマイナスになっている波長域があることに気がつきますね。( r ( λ ) の 435.8 ~ 546.1 nm の波長域が特に目立ちます。≪※3≫ )
等色するための混色比を示す値がマイナスというのは一体どういうことなのでしょうか?
これは、この波長域の単色光の色 F ( λ ) に対しては、実在の三原色[ R ]、
[ G ]、[ B ]の混色比をどのように変えてみても、単色光 F ( λ ) の方が鮮やか過ぎて等色できないことを示しています。このように如何にしても等色できない場合、三原色の内のどれかを試料光 F ( λ ) 側へ移動させて試料光と混色させるという操作をしてやれば、右側視野の残りの二原色の混色と等色できる条件を作り出すことができます。
例えば、(青緑色に見える)波長 λ = 500 nm の単色光 F ( 500 ) の場合、これに原色の赤[ R ]を r ( λ ) = 0.072 だけ混色し、 更に右視野の緑[ G ]と
青[ B ]を g ( λ ) = 0.085、b ( λ ) = 0.048 という比率で混色すれば、両視野の色が一致しますので、
F ( λ ) + r ( λ )・[ R ]≡ g ( λ )・[ G ]+ b ( λ )・[ B ]
という等色式が得られます。この等色式の r ( λ )・[ R ]を右辺に移項してやれば
F ( λ ) ≡- r ( λ )・[ R ]+ g ( λ )・[ G ]+ b ( λ )・[ B ]
となります。
これが、 波長 λ = 500 nm で等色関数 r ( λ ) がマイナス表記される理由です。

RGB 表色系の色度図 ( r g 色度図)
このようにして得られた等色関数 r ( λ ) 、 g ( λ ) 、 b ( λ ) によって、三原色 [ R ]、[ G ]、[ B ]による刺激値 R 、G 、B が定義されます( k は定数 )。
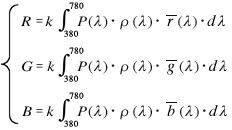
これより
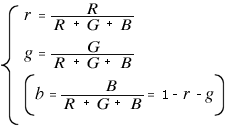
とすると、r は全刺激量に対する赤の刺激量の比、g は全刺激量に対する緑の刺激量の比、b は全刺激量に対する青の刺激量の比を示します。ここで、r を横軸に、g を縦軸にとって色度図を描くと下図のようになり、これを r g 色度図と言います≪※4≫。

この r g 色度図の曲線部分は単色光軌跡(またはスペクトル軌跡)と呼ばれ、図中に示した数値はその座標位置に対応する単色光の波長を示しています。また、単色光軌跡の曲線両端(可視域の両端の単色光の色度点)を結ぶ直線を純紫軌跡と呼びます。純紫軌跡上には単色光の色度点は存在せず、可視域両端の単色光の加法混色の結果として得られる色の色度点として得られるものです。
世の中のすべての色は、この曲線(単色光軌跡)と直線(純紫軌跡)で囲まれた領域内の色度点で表され、例えば、三原色を均等に混色してできる無彩色はW+で示した位置
( r , g )= ( 0.333 , 0.333 )
になります。
r g 色度図を見ると、第2象限( r < 0 、g > 0 ) の領域に色度域が大きく張り出しているのが目立ちます。この領域は
r < 0 すなわち R < 0 ですから、上述のように、実在する三原色 [ R ]、[ G ]、[ B ]の加法混色では作り出せない色・・・・・その色に赤原色 [ R ] を混色すれば、緑原色 [ G ] と青原色 [ B ] を混色した色と等色できる色・・・・・を示す領域です。
このように、RGB 表色系は、等色関数が負の値になる(混色比が負になる)波長域があって直感的に分かりにくく、また、負の刺激量が混在するということは(1931年当時は今のような計算器も無かったこともあって)計算が結構煩雑という問題がありました。
そこで、等色関数がすべて非負(マイナスの値とならない)となるような仮想の原刺激[ X ]、[ Y ]、[ Z ] を設定し、この仮想の三原色による XYZ 表色系が作られました。

原刺激 [ X ]、[ Y ]、[ Z ] は、上図のような r g 色度図の表色領域に外接する三角形を想定し、その頂点で示される仮想の色(虚色)となります。こうすれば、表色領域の中の全ての座標点は、
[ X ]、[ Y ]、[ Z ] の非負の混色比で表示することが可能になります。
この図の [ Y ] と [ Z ] を結ぶ直線が縦軸に、[ Z ] と[ X ] を結ぶ直線が横軸になるように座標変換してやれば、全ての表色領域が、直交座標の第1象限内で表現することが可能になります。また、更に「明度」に関する条件として
y ( λ ) ≡ V ( λ ) を加えて座標変換して得られた色度図が XYZ 表色系の x y 色度図(右図)です。≪※5≫

三刺激値 X、Y、Z と 視細胞( L 、 M 、 S 錐体)との関係
上述のように座標変換した結果、RGB 表色系の三刺激値 R、G、B と XYZ 表色系の三刺激値 X、Y、Z の間には以下の式で表される関係があります。
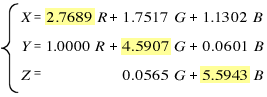
この関係式の、 R、G、B の係数の大きさに注目して下さい。黄色で着色した係数が他の係数に比べて突出して大きいことが分かります。つまりこれは、刺激値 X は R が主成分になって、それに幾分かの G と B の成分が加味されていることを示しています。同様に、刺激値 Y は G が主成分で、R と B が幾分加味されたものであり、刺激値 Z は B が主成分で、G が幾分加味されているということです。これは、XYZ 表色系の等色関数 x ( λ ) 、 y ( λ ) 、 z ( λ ) のグラフと対応させて見ればよくわかるかと思います。別の表現をすれば、刺激値 X は、視細胞の L 錐体の応答が主成分で、それに M 錐体、 S 錐体の応答が加味されたもの、刺激値 Y は M 錐体の応答が主成分でそれに L 錐体と S 錐体の応答が加味されたもの、刺激値 Z は S 錐体の応答が主成分で M 錐体の応答が加味されたものと言うことができます。

以上のように、CIE 表色系は、人間の視細胞(錐体)の働きに基く色覚特性を科学的実験によって特性づけたデータを基礎にして構築された表色系であると言えます。
注釈
≪※1≫ CIEが設定した単色光三原色の波長
これら三原色の選定については、1931 年当時に比較的容易に利用できた水銀の輝線スペクトルから、
青 ( λ B = 435.8 nm ) と 緑 ( λ G = 546.1 nm ) の原色として、また、赤の原色は、実用上一定以上の色感覚を引き起こす可視域最長のキリのよい波長を選定したようです。
≪※2≫ 等色関数と観察視野角度( 2° 視野 と 10° 視野) ・・・・・ 色の面積効果
試料色の占める面積(視野角の大きさ)によって、ヒトの眼には色の見え方が微妙に異なって見えることが分かっています。これを「色の面積効果」と言っています。これは、網膜上で視細胞(錐体)が集中分布する中心窩部分(ほぼ視野角 2° に相当)のみが黄斑色素で覆われており、黄斑部以外の網膜領域と色覚特性がわずかに異なっていることが原因です。
従って、色を正確に評価するためには、視野角の大きさを規定し、その条件に適した等色関数で評価しなければなりません。1931 年に規定されたのは 2° 視野の等色関数でしたが、その後の運用および研究の結果、もっと大きい視野角(広い試料面積)での評価条件規定が必要であることがわかり、1964 年にその代表条件として 10° 視野の等色関数 x10 ( λ ) 、y10 ( λ ) 、z10 ( λ ) が決められました。本文中で図示した RGB 表色系の等色関数は 2° 視野のものです。なお、視野角が 4° 以下の場合は 2° 視野の等色関数を、4° を超える場合は 10° 視野の等色関数を用いることになっています。

≪※3≫ 負の等色関数
r ( λ ) の 3 つの関数の中で、マイナスの値となるのは r ( λ ) が最も目立ちますが g ( λ ) 、b ( λ ) 、についても、ほんの僅かながらマイナスの値となる波長域が存在します。
≪※4≫ 色度図上での 3 原色の座標
r , g , b の 3 つの変数がありますので、本来は r 軸、g 軸、b 軸の3次元直交座標で表示されるのですが、b の値は r と g の値が決まれば自動的に決まりますから r - g 平面のみで色度を表示できることになります。各原色の座標は対応する軸上の切片 1 の位置に表示されます。
つまり、原色 [ R ] は( r , g )=( 1 , 0 )、原色 [ G ] は( r , g )=( 0 , 1 )となります。
また、原色 [ B ] は b = 1,r =g = 0 ですから、rg 色度図上では原点すなわち ( r , g )=(0 , 0) になります。
≪※5≫ RGB 表色系から XYZ 表色系への座標変換
XYZ 表色系は、RGB 表色系が負の刺激値(負の等色関数)をもつことの解りにくさや不便の解消を主目的としたものですが、更に、もう一つ、「明るさ」を評価する関数である標準分光視感効 V ( λ ) に等色関数の内の y ( λ ) を一致させることを座標変換条件にしたことが大きな特徴として挙げられます。こうすることによって、色の心理的三属性の「色相」と「彩度」の組み合わせを色度座標 ( x , y ) に対応させ、「明度」を刺激値 Y に 対応させた訳です。

歴史的に見れば、先ず、一次元情報である「明るさ」に対する研究が行われて標準分光視感効率 V ( λ ) が確立され、その後を追うようにして、(色相・彩度・明度の)3 次元情報である色彩の研究が進行しました。その中で、「色彩」を定量表示するシステムを構築する時点で、すでに確立されていた「明るさ」の定量的評価関数である V ( λ ) を取り込んで色の表示システムを構築したというのは、極めて自然な流れであったと言えますね。